Kalin's Blog

【Image Processing】Morphology 形態學

發表於 更新於 分類於

本篇為形態學影像處理的筆記，會簡單介紹一些形態學影像處理方法，如：膨脹處理（Dilation）、侵蝕處理（Erosion）、開與合運算（Opening & Closing）與形態學濾波（Morphological Filtering）。

What is Morphology？

在數學上的形態學（Mathematical morphology）是一門建立在格論和拓撲學基礎之上的圖像分析學科，也就是本篇拿來做影像處理的基本理論。

Morphology 非常實用，且可以運用的範圍非常廣泛，如：邊界抽取、區域填充、細線化、粗線化、型態梯度、型態濾波、高帽轉換……等。

基本概念

主要運用集合運算與邏輯運算。（集合運算與邏輯運算雖然概念同構，但不完全相同）
理論會使用集合運算解釋，而程式實作則是使用邏輯運算。

邏輯運算

  • 基本邏輯：AND、OR、NOT，其真值表如上圖。
    • 分別對應到集合運算中的交集、聯集、補集。
  • 而在高職的數位邏輯中有學到，其餘的 XOR、NAND、NOR 等都可用基本邏輯組成。

集合運算

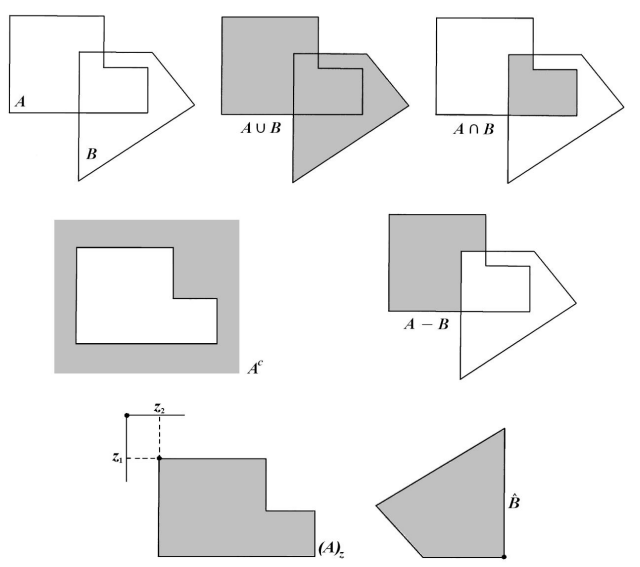
  • 基本的交集（Intersection）、聯集（Union）。
  • 補集（Complement）： A 的補集是影像G中所有不屬於 A 的元素集合。
    • $A^{c} = \lbrace\ w\ |\ w \in G\ and\ w \notin A\ \rbrace$
  • 差集（Difference）：
    • $A - B = \lbrace\ w\ |\ w \in a\ and\ w \notin B\ \rbrace = A \cap B^{c}$
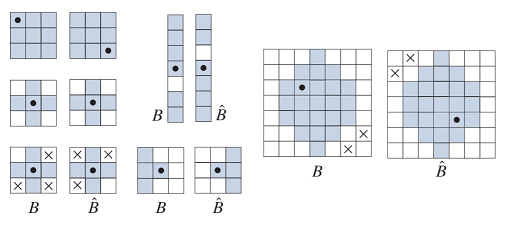
  • 反射集（Reflection）：B 集合中所有元素相對集合原點（不一定是影像座標原點）的反射值之集合。
    • $\hat{B} = \lbrace\ w\ |\ w = -b,\ b \in B\ \rbrace$
    • 雖然上方有圖示，但這邊額外補充其他圖示，應該會更清楚。
  • 平移運算（Translation）：
    • $(A)_z = \lbrace\ c\ |\ c = a + z,\ for\ a \in A\ \rbrace,\ z = (z_1,z_2)$
      • $\begin{cases} c_1 = a_1 + z_1 \\ c_2 = a_2 + z_2 \end{cases}$

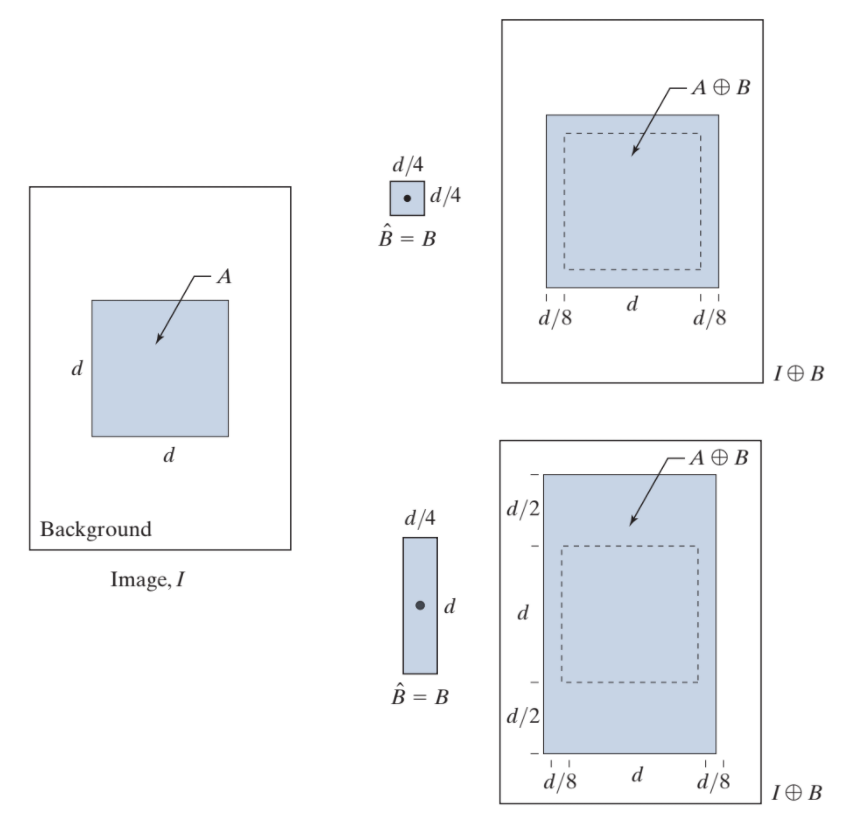
膨脹處理（Dilation）

定義如下：
$A \oplus B = \lbrace\ z\ |\ (\hat{B})_z \cap A \neq \varnothing \rbrace $

實作上可以理解為：

  • A 是我要 Dilation 的目標。
  • B 一般稱為 Struceures Element，可以理解為 Dilation 作用在每一點的遮罩（mask）大小（m * m 或 m * n）。
  • 等式右邊意思是「把 B 做 Reflection 後在集合內平移且跟 A 不是空集合的部分做 AND」。
    • Note：若 Structure Element 為上下左右皆對稱，則 Reflection 的動作可以忽略。

而稍微轉換個角度思考，我們也可以將定義改寫如下：
$A \oplus B = \lbrace\ z\ |\ [\ (\hat{B})_z \cap A\ ]\ \subseteq A \rbrace $

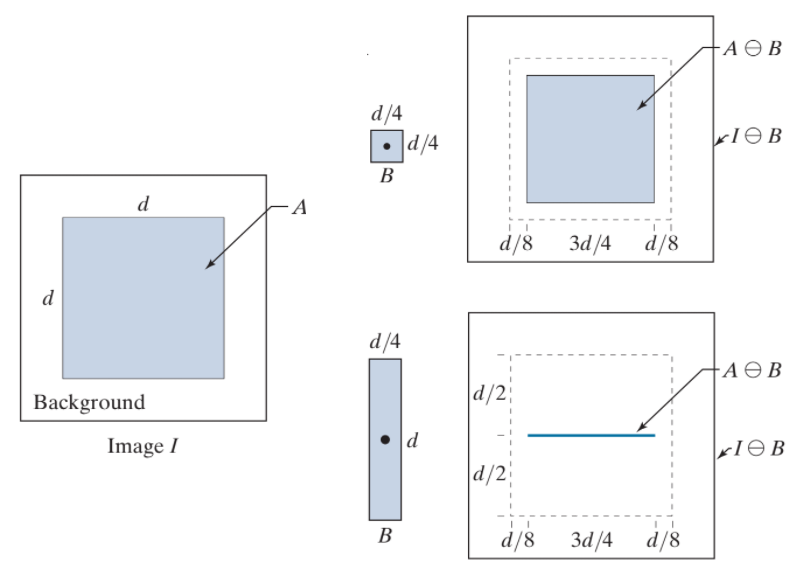
侵蝕處理（Erosion）

定義如下：
$A \ominus B = \lbrace\ z\ |\ (B)_z \cap A^{c} \neq \varnothing \rbrace $

基本上概念跟 Dilation 大致相同，只是反過來做而已。
而經由上面定義會發現 $B_z$ 其實一直在 $A$ 內，且跑出來的樣子就是結果了，因此我們也可以將定義改寫如下：
$A \ominus B = \lbrace\ z\ |\ (B)_z \subseteq A\ \rbrace $

斷開與閉合運算（Opeing & Closing）

建立在 Dilation 與 Erosion 的運算基礎上，簡單來說：

  • Opening：先 Erosion 再 Dilation。 $ A \circ B = (A \ominus B ) \oplus B$
  • Closing：先 Dilation 再 Erosion。 $ A \bullet B = (A \oplus B ) \ominus B$

斷開運算 Opening

先做 Erosion 再做 Dilation。其數學式如下：
$ A \circ B = (A \ominus B ) \oplus B = \bigcup\ \lbrace\ (B)_z\ |\ (B)_z \subseteq A\ \rbrace$

其作用等同是拿 Structures Element 在目標內部任意移動，而若是 Structures Element 到不了的地方就會被消除掉，可以將圖形凸出的銳角給鈍化。

Opening 具有以下特性：

  • $A \circ B$ 是 $A$ 的子集合。
  • 若 $C$ 是 $D$ 的子集合，則 $C \circ B$ 是 $D \circ B$ 的子集合。
  • $(A \circ B) \circ B = A \circ B$

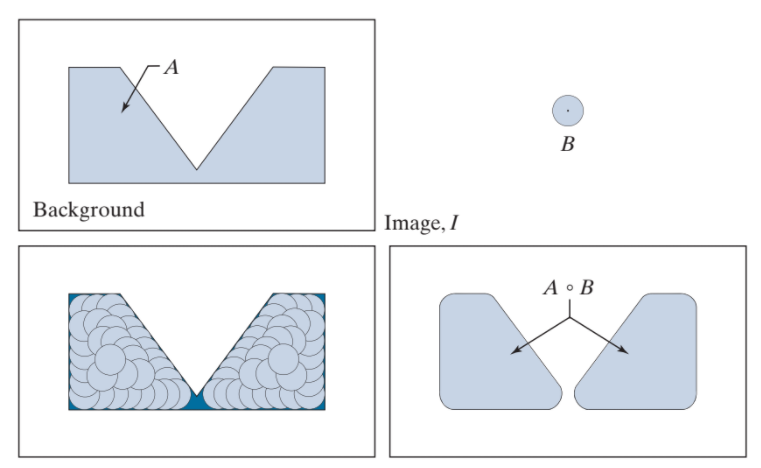
閉合運算 Closing

先做 Dilation 再做 Erosion。其數學式如下：
$ A \bullet B = (A \oplus B ) \ominus B = \lbrace\ (B)_z\ |\ (B)_z \cap A \neq \varnothing\ \rbrace$

其實就是 Opening 反過來做而已。等同是拿 Structures Element 在目標外部移動，進不去的地方就把它填滿，可以將圖形內陷的銳角給鈍化。

Closing 具有以下特性：

  • $A$ 是 $A \bullet B$ 的子集合。
  • 若 $C$ 是 $D$ 的子集合，則 $C \bullet B$ 是 $D \bullet B$ 的子集合。
  • $(A \bullet B) \bullet B = A \bullet B$

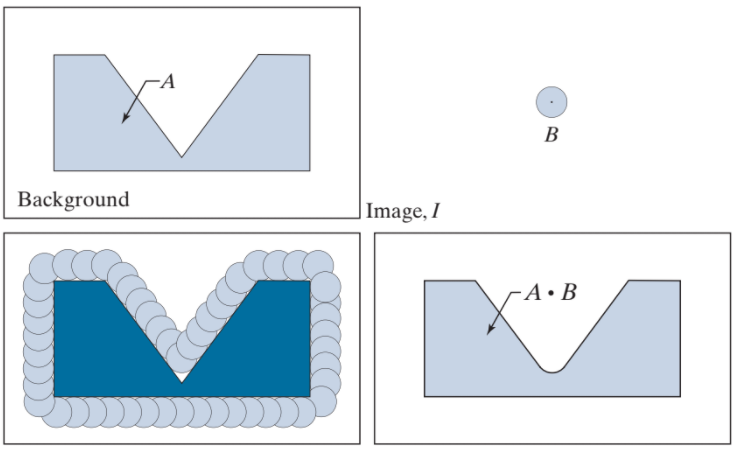
應用：形態學濾波（Morphological Filtering）

情境1

如下圖所示，該指紋圖片有一些白色雜訊，我們想要在不影響指紋型狀的狀況下去移除雜訊。而此時就可以使用「型態學濾波」了！其流程皆由圖上文字所述。

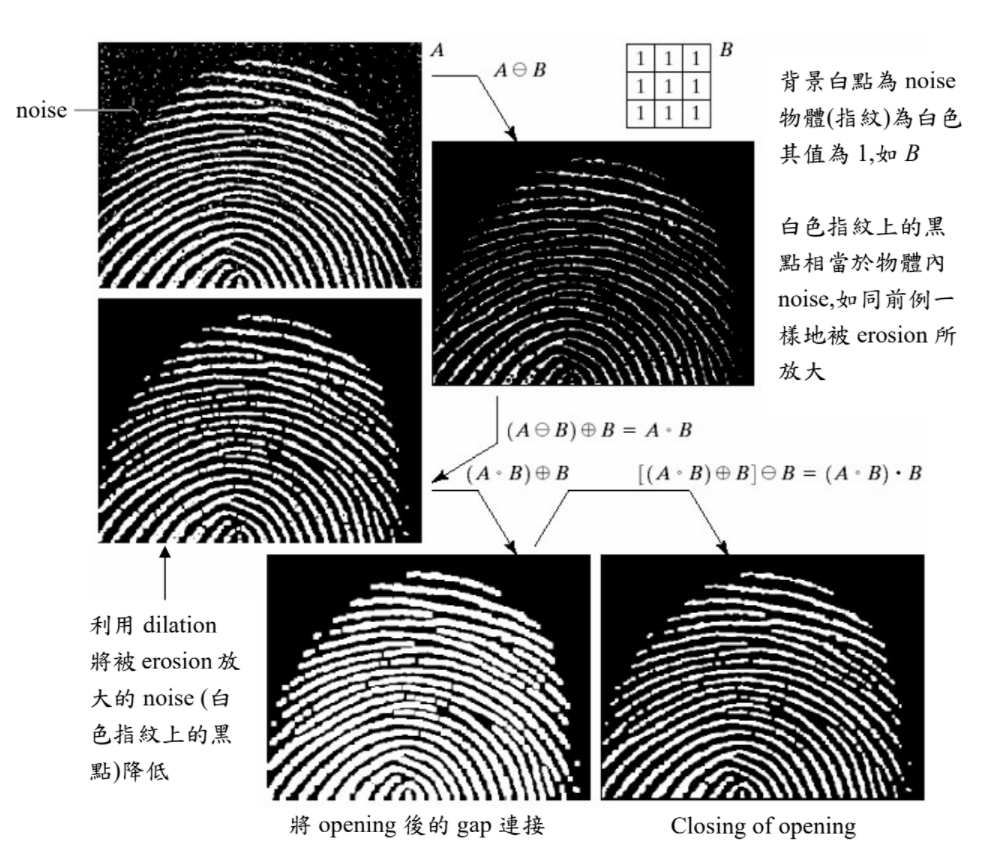
情境2

又或者有另一種情境，我們可以看到下圖最左邊那張，裡面有大大小小不同的方點（有1 * 1、3 * 3、5 * 5、7 * 7、9 * 9、15 * 15 等 6 種尺寸），今天我們希望把 15 * 15 的方點留下，而其他東西就是我們不要的雜訊，要將他們濾掉。

我們可以設計一個 11 * 11 or 13 * 13 or 15 * 15 的 Structures Element 去跟它做 Erosion，結果會長的像下圖中間那張。
而利用 Erosion 的原理，小於 Structures Element 的方點會直接被侵蝕到不見，以 13 * 13 的 Structures Element 我們想要留下的目標會被侵蝕到變成 3 * 3 的方點（若用 11 * 11 會變 5 * 5；用 15 * 15 會變 1 * 1），這樣我們確實將不必要的雜訊去除了，但是最終我們不希望改變目標的原始大小，因此可以再用同一個 Structures Element 去做 Dilation 將目標膨脹回原來的尺寸，如下圖最右邊那張。

形態學影像處理其實還有非常多應用，而「形態學濾波」只是其一種。而因為剛好最近碰到，因此本篇僅記錄此應用，至於其他的應用，未來若有機會再補上文章。

程式碼

最後附上在寫這篇文章時所寫的Code，我都放在GitHub內了。
其功能有 Dilation、Erosion、Opening 及 Closing，且可以調整大小。

References

AdSense